Trabajo de GeoGebra
·
Triángulos
1.1 Propiedades y tipos de triángulos.
1- Un lado de un triángulo es menor que la suma de los
otros dos y mayor que su diferencia.
2- La suma de
los ángulos interiores de un triángulo es igual a 180°.
3- El valor de un ángulo exterior es igual a la suma
de los dos interiores no adyacentes.
Tipos de triángulos. Los triángulos se
pueden clasificar:
v Según la medida de sus lados (2ª fila del dibujo1)
o
Equilátero: Tiene iguales sus tres lados y son iguales sus ángulos
interiores.
o
Isósceles: Tiene dos lados iguales y uno desigual. Los dos
ángulos de los lados iguales son iguales también y el distinto agudo.
o
Escalenos: Tiene diferentes sus tres lados y sus tres ángulos.
v Según la medida de sus ángulos ( 1ª fila del dibujo1)
o
Obtusángulo: Un ángulo obtuso (> 90 grados) y los otros dos
ángulos agudos (< 90 grados).
o
Rectángulo: Un ángulo recto (= 90 grados) y dos ángulos agudos
(< 90 grados). Los lados que forman el ángulo recto se
llaman catetos (c y b), el otro lado hipotenusa.
o
Acutángulo: Tres ángulos agudos (< 90 grados)
1.2 Rectas y
puntos nobles en el triangulo.
Sabiendo
que la altura de un triángulo es cada una de las rectas perpendiculares
trazadas desde un vértice al lado opuesto (o su prolongación) a dicho vértice.
- Ortocentro
El ortocentro
de un triángulo es el punto de intersección de las tres alturas del triángulo
(siendo una altura el segmento que parte de un vértice y es perpendicular al
lado opuesto a dicho vértice). Entonces para representar gráficamente el
ortocentro de un triángulo dibujamos las tres alturas y nos quedamos con el
punto en el que se intersecan. En esta figura puede verse el ortocentro de un triángulo:
- Incentro
El incentro es el centro de la
circunferencia inscrita al triángulo, por lo que la distancia a cada uno de sus
lados es la misma (el radio de dicha circunferencia). Más concretamente, es el
punto de intersección de las bisectrices de cada uno de los ángulos del triángulo
(siendo una bisectriz la recta que divide a un ángulo en dos ángulos
iguales), por lo que para representarlo gráficamente debemos dibujar las tres
bisectrices y localizar el punto de intersección de las mismas. En la imagen
siguiente podéis verlo:
- Baricentro
El baricentro (también llamado centroide)
de un triángulo es el punto de intersección de las medianas de dicho triángulo
(siendo una mediana el segmento que une un vértice con el punto medio
del lado opuesto). Por ello, para representar gráficamente el baricentro
debemos dibujar las tres medianas y localizar el punto en el que se cortan.
Esta figura muestra el baricentro de un triángulo:
- Circuncentro
El circuncentro de un triángulo es el
centro de la circunferencia circunscrita al triángulo, por lo que la distancia
a cada uno de sus vértices es la misma (el radio de dicha circunferencia). En
concreto, es el
punto de intersección de las mediatrices del triángulo (siendo
una mediatriz la recta perpendicular a
un lado que pasa por el punto
medio del mismo). Por tanto, para representar gráficamente el
circuncentro
dibujamos las tres mediatrices y localizamos el punto de intersección de las
mismas.
Puede verse el circuncentro de un triángulo en la siguiente imagen:
Recta de EULER
El ortocentro, el baricentro y el
circuncentro de un triángulo no equilátero están alineados; es decir,
pertenecen a la misma recta, llamada recta de Euler.
1.3 Teorema de Pitágoras.
En
un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los
cuadrados de los catetos.
1.3.1. Demostración gráfica.
En
un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los
cuadrados de los catetos.
h2 = b2 + c2
1.3.2. Teorema en 3D.
Aplicaciones del
teorema de Pitágoras:
1.-
Conociendo los dos catetos calcular la hipotenusa
3.- Conociendo sus lados, averiguar si es rectángulo
Para que sea rectángulo el cuadrado de lado mayor ha de ser igual a la suma de los cuadrados de los dos menores.
L2=l2+l2 (L= Lado mayor; l = lado menor)
Aplicaciones del teorema de Pitágoras
1.- Diagonal del cuadrado
n= B-b
4.- Altura del trapecio isósceles
n= B-b/2
5.- Altura del triángulo equilátero

6.-Apotema de un polígono regular
7.- Apotema del hexágono inscrito
l = r
8.- Lado de un triángulo equilátero inscrito
9.- Lado de un cuadrado inscrito
1.4. Teorema de Thales
Si dos
rectas cualesquiera se cortan por varias rectas
paralelas, los segmentos determinados en una de las rectas son proporcionales a
los segmentos correspondientes en la otra.
No he podido
quitar los puntos, no los tengáis en cuenta. La T y S son dos rectas cortadas por
tres rectas paralelas. Lo que dice el teorema es que el segmento AB es
semejante al segmento A2B2, y el segmento BC es semejante al segmento B2C2, a
su vez son semejantes los segmentos AC y A2C2.
Teorema
de Thales en un triángulo
Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triangulo, se obtiene otro triángulo AB'C', cuyos lados son proporcionales a los del triángulo
ABC.
La misma relación de semejanza entre
segmentos AB y AB1, AC y AC1 y BC y B1C1
Semejanza de triángulos
Dos triángulos son semejantes cuando
tienen sus ángulos homólogos iguales y sus lados homólogos proporcionales.
La razón de la proporción entre los
lados de los triángulos se llama razón de semejanza.
Criterios de semejanza de triángulos
Se dice que dos
triángulos son semejantes si cumplen alguno de estos criterios, dos o los tres.
3
Dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo
comprendido entre ellos igual.
Aplicaciones
de la semejanza de figuras. Cálculo de la altura de un objeto
Para
medir alturas de objetos a los que no podemos acceder se puede utilizar
semejanza de figuras.
Se
hace que la altura que queremos calcular forme parte de un triángulo rectángulo
del que se conoce un lado. Se construye otro triángulo semejante al anterior
con longitudes conocidas. La medida de los lados del triángulo pequeño y las
del grande son proporcionales:
Altura
desconocida/BC = A´B´/B´C´
Ejemplo: Calcular
la altura de un árbol a partir de su sombra.
Un árbol proyecta una sombra de 5 m. a la misma hora
una persona de 1.70 m de altura proyecta
una sombra de 50 cm. ¿Cuál es la altura del árbol?
La
altura y la sombra, tanto de la persona como del árbol, forman entre ellas un
ángulo recto. Consideramos entonces el triángulo que se forma uniendo sus
extremos.
Unificamos
las unidades y expresamos la proporción entre los lados.
Altura
árbol/sombra árbol= altura persona/sombra persona
h árbol / 5m = 1,70 m / 0,5 m
h árbol = 7 x 1,70 / 0,5
h árbol = 17 m

















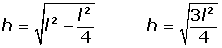






























No hay comentarios:
Publicar un comentario